逻辑斯蒂回归总结

一、背景

Logistic回归来源于线性回归，线性回归是用一个线性函数去拟合一些点，如果我们想进行分类的话，那就只需要找一个单调可微的函数，将分类任务的真实标记和回归模型的预测值联系起来。

对于二分类任务，其输出标记是0和1，而回归模型的预测值z = wTx + b是实数，于是我们需要一个函数将实数转换为0/1值。最简单的方法，就是使用阶跃函数，大于0判为1，小于0判为0。但是单位阶跃函数不连续，我们希望有一个近似单位阶跃的函数，而且单调可微，对数几率函数就是这样一个常用的替代函数，即Logistic函数。

Logistic回归与多重线性回归实际上有很多相同之处，最大的区别就在于它们的因变量不同，其他的基本都差不多。正是因为如此，这两种回归可以归于同一个家族，即广义线性模型（generalizedlinear model）。

这一家族中的模型形式基本上都差不多，不同的就是因变量不同。

• 如果是连续的，就是多重线性回归；
• 如果是二项分布，就是Logistic回归；
• 如果是Poisson分布，就是Poisson回归；
• 如果是负二项分布，就是负二项回归。

Logistic回归的因变量可以是二分类的，也可以是多分类的，但是二分类的更为常用，也更加容易解释。所以实际中最常用的就是二分类的Logistic回归。

二、模型

1、构造预测函数h

Logistic回归虽然名字里带“回归”，但是它实际上是一种分类方法，主要用于两分类问题（即输出只有两种，分别代表两个类别），所以利用了Logistic函数（或称为Sigmoid函数），函数形式为：

对于线性边界的情况，边界形式如下：

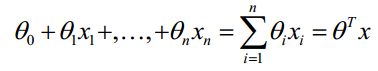
构造预测函数为：

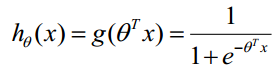
函数 的值有特殊的含义，它表示结果取1的概率，因此对于输入x分类结果为类别1和类别0的概率分别为：

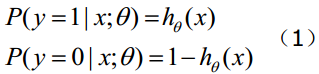
2、构造似然函数

取似然函数如下：

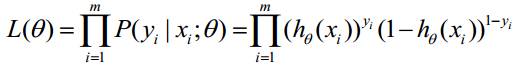
对数似然函数：

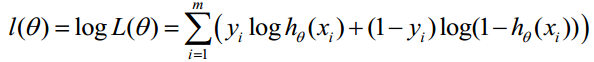
最大似然估计就是求使 取最大值时的参数θ，这里实际上可以使用梯度上升法来求解最大值，但是一般都取负数然后用梯度下降法估计 的最小值来求解：

所以实际上可以把J看成Logistic回归模型的损失函数。一般来说，在实际应用中，logistic会配合正则化使用，特别是L1正则化。

3、梯度下降法求的最小值

θ更新过程：

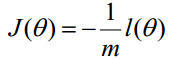
θ更新过程可以写成：

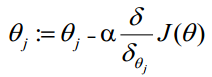
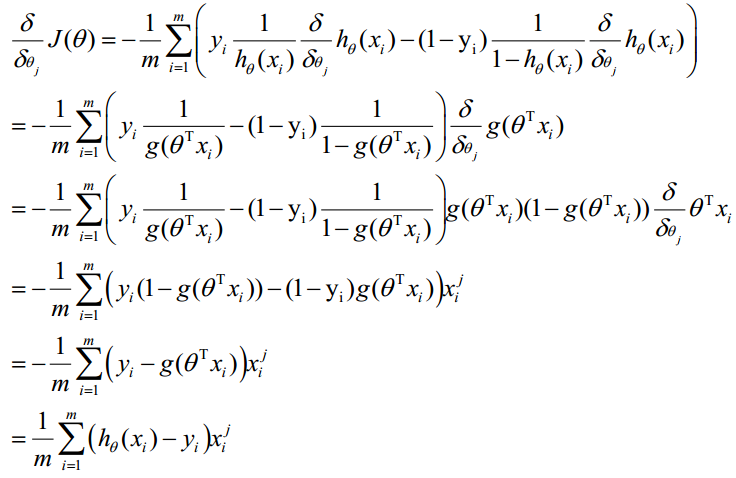
4、求解过程

除了可以用上述的梯度下降法来求解，一般还可以用牛顿法、拟牛顿法等来进行求解。

三、应用

Logistic回归的主要用途：

• 寻找危险因素：寻找某一疾病的危险因素等；
• 预测：根据模型，预测在不同的自变量情况下，发生某病或某种情况的概率有多大；
• 判别：实际上跟预测有些类似，也是根据模型，判断某人属于某病或属于某种情况的概率有多大，也就是看一下这个人有多大的可能性是属于某病。

Logistic回归主要在流行病学中应用较多，比较常用的情形是探索某疾病的危险因素，根据危险因素预测某疾病发生的概率，等等。例如，想探讨胃癌发生的危险因素，可以选择两组人群，一组是胃癌组，一组是非胃癌组，两组人群肯定有不同的体征和生活方式等。这里的因变量就是是否胃癌，即是或否，自变量就可以包括很多了，例如年龄、性别、饮食习惯、幽门螺杆菌感染等。自变量既可以是连续的，也可以是分类的。

四、问题

介绍Logistic回归的原理？

Logistic是一种广义的线性模型，其决策面是一个超平面。他在线性分类器的基础上，引入了sigmoid函数来将分类器的值映射到类别0和1,而不是使用简单的阶跃函数来进行判断。Logistic回归的优化目标是最大化其对数似然函数，而最大化的过程一般使用梯度下降法、牛顿法等进行实现。所以它并不是一个回归模型，而是一个二分类问题。

Logistic为什么要引入sigmoid来做映射？

（1）为什么要做映射？

因为线性回归的结果是一个数值，不能直接用于分类，所以我们考虑使用一种策略来将其计算的结果映射到一个概率上，便于进行分类。

实际上映射只是一种分类的策略，对于一般的线性分类器，如感知机，其做法就是认为y>0为正类，y<0为负类，这是一种非常简单的策略，是从几何上来对分类进行解释，其优化的目标就是最小化分类的损失。而对于SVM，其策略就是从几何上来解释，它并不考虑每个点被划分到每个类的概率，而是和感知机一样，认为函数值>0为正类，<0为负类，在优化的过程中，加入了对分类面的约束，取点到分类面距离最小的分类器作为最优的分类平面，离分类面最近的点认为是支持向量，其优化的目标就是最小化分类器的间隔，或者是最小化合页损失。

（2）为什么要使用sigmoid做映射？

一方面，sigmoid函数具有非常优良的性能，其导数和它自身存在一定的关系，利于后续利用梯度下降法进行求解，计算起来也会飞快；

另一方面，sigmoid函数在两边变化缓慢，中间变化迅速，对于分类边界附近的点，应该具有更高的分辨能力。

Logistic回归的好处？

• 计算代价不高，易于理解和实现
• LR相比SVM，更适合海量数据的处理
• 可以拓展为多分类

对比一下Logistic回归、SVM、Perception等？

相同点：

• 都是分类模型。

不同点：

• Logistic回归、perception都是线性分类器，而SVM在引入kernel方法之后，变成了非线性的模型。

• 优化的目标不一样，Logistic回归是基于概率的模型，其最优化的目标是最大化模型的对数似然函数，一般用梯度下降或者牛顿法求解；SVM和perception可以认为都是基于几何的模型，特别是SVM，它优化的目标都是期望误差，即经验风险，SVM是合页损失函数，而Perception就是分类的损失函数。Perception基于样本在分类面的两边的位置来分类，而SVM则将分类的边界拉大，用间隔之外的位置用于分类。

• Logistic回归中，每个点对分类面都不会有影响，点对分类面的影响会随着距离的增大而指数衰减；Perception中每个点都影响分类，但每个点对于分类面的影响，可以认为和距离无关；而SVM中，对分类面有影响的只有边界附近的支持向量。

• LR可以拓展为多分类，而SVM和Perception不行。

如何选择SVM和Logistic回归?

• 如果Feature的数量很大，跟样本数量差不多，这时候选用LR或者是Linear Kernel的SVM

• 如果Feature的数量比较小，样本数量一般，不算大也不算小，选用SVM+Gaussian Kernel

• 如果Feature的数量比较小，而样本数量很多，需要手工添加一些feature变成第一种情况